Smith-Waterman算法的简单Perl实现（糊作业用）

写在前面

学习双序列比对时肯定会学Needleman-Wunsch算法和Smith-Waterman算法，肯定是绕不开的。原理和计算都很简单的，因此作为生信课程的一部分，老师很可能会让你利用代码来实现这两个算法。这也无可厚非，毕竟生信这个傻逼专业和纯生物的核心区别就是你平时要把很多时间精力浪费在写一些只要识字的人现用现学都能写出来的代码上，然后靠这点计科人不屑于写的破代码去在其他天坑专业面前装装样子。咳……
其实利用代码来实现也并不难，从生信人必备的Python、R、C++里任选一门语言，打开浏览器，搜索“XX算法的XX实现”，一般情况下都能搜到。然后只要改个变量名，再利用聪明才智润色一下，就可以上传提交了，反正老师也不看。
但是当你只会一个全天下可能只有玩Bioinfor的那么一小撮人在用的perl语言里面的一点点低端操作，而中文互联网上又搜不到“Smith-Waterman算法的perl实现”时(夸张一下别当真)，你该怎么办？

---

一、前言

本文很大程度上借鉴了这位大佬的文章：https://blog.csdn.net/qq_45091883/article/details/106507494

虽然这位作者写的是Needleman-Wunsch的perl实现，但是思想值得借鉴，因为两个算法主体上是相通的，所以我很大程度上参照了这篇文章（主要是就这一个看得懂，哭死）。感谢这位作者的原创内容和非常详尽的注释，不过您确实也有几个地方写错了。

另外还有：某外国网站的英文教程 和 某可能是国内大佬写的英文教程
其实说互联网上搜不到Smith-Waterman算法的perl实现那是不可能的，但是我搜了半天找到的还是两个英文的。其实英文倒也没什么，也不是不能看。只是这两个作者的代码，一个一行解释说明的注释也没有，给你的perl老师看他都不一定看得懂；另一个则可能是想要实现很多高端的操作吧，写得太复杂了，如果你只是想实现一下算法的核心步骤看他那个反而可能会越看越看不懂，然后虽然有注释但是是全英文的，我这种6级连600都没考到的铁five根本看不懂捏。

看到这里你可能会想问：你这BYD不就是糊个作业吗，难的英文的你不愿意看，简单的你又说找不到，perl语言找不到你不能用Python写？R,C不也行?这些语言都不会你学你马的生信。
确实，这里先给各位精通各种语言的爷磕三个响头。1，2，3。首先，Python我正在学，R和C++早就学过了，但是时间长搞忘了；perl因为这学期手贱选了，最近刚学完，印象比较深刻（虽然会的不多）；而且个人认为，学校布置的题目自己写一写把核心内容实现了就已经够了，没有必要去搞一大堆纷繁的操作去显摆你的打字水平，自认为自己的水平不足以支持自己写出这份完整的代码，所以先上网搜了一下，刚好看到了别人的方法不错，就拿来用了。虽然我说是糊作业用的，但还是经过了一点思考，个人虽然成绩不好，但是自尊心还是有的，没办法允许自己照搬别人的代码。

二、代码

这份代码不尽完善，只是实现了对两条给定序列的Smith-Waterman算法比，如果是拿来糊个作业，那纯纯是太够了。想要更高端一点，卖弄一下I/O也是可以自己加的。不保证一定正确，有错误请指正（暗示来点评论）

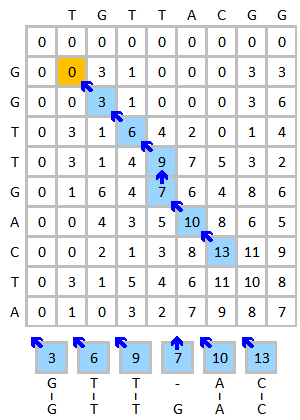
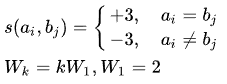
注意：
1. 本代码利用了Smith-Waterman局部匹配的是最优结果这个特点，从而省去了中间回溯时判断是否存在分支的步骤，不清楚是否会有影响
2.在使用代码时应该仔细参照一下打分矩阵的图，而且两条序列若是长度不同的话定义循环时不能将两个长度写反
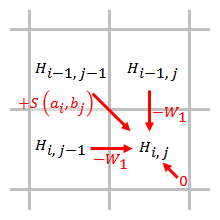
3.在Smith-Waterman算法中比较最大值是不仅是三个方向的前值，还要加上0，因此最小也不能为负值。

# Smith-Waterman using Perl
# produced by  LYS/mashiro_munetani
# 2022 11.13

use List::Util qw(max); # 后面需要使用max函数
my $s1="TGTTACGG";# 输入你要比较的两条序列，注意一下s1是打分矩阵中横向的序列，s2是纵向的
my $s2="GGTTGACTA";
my @ss1=split("",$s1);
my @ss2=split("",$s2);

my $len1=length($s1);
my $len2=length($s2);

my @score=();# 定义并初始化得分矩阵
my @back=();# 用于回溯的矩阵，利用赋值的方式记录每个位置的值是从何处来的
$score[0][0]=0;
$back[0][0]=0;

for my $i(1..$len2){ # Smith-Waterman要求打分矩阵第一行和第一列都为0，注意这里的两条序列长度不同，要逆转后分别赋值
    $score[$i][0]=0;
     $back[0][$i]=4;# 每个位置的值来源于左边：赋4（参照了那篇博客里作者的方法）
                                   # 至于为什么不是3，因为可能会出现上方和对角线方向得到的值相等的情况
}

for my $i(1..$len1){ 
  $score[0][$i]=0;
  $back[$i][0]=2; # 每个位置的值来源于上面：赋2 
}


sub get_score{ # 设置子函数获取对角线方向的得分,哈希存放一下对角线的匹配得分结果
    my %all=("AA"=>3,"CC"=>3 ,"GG"=>3, "TT"=>3,
			"AC"=>-3, "AG"=>-3,  "AT"=>-3, 
			"CA"=>-3,  "CG" =>-3,  "CT" =>-3, 
			"GA" =>-3,  "GC" =>-3,  "GT" =>-3, 
			"TA" =>-3,  "TC" =>-3,  "TG" =>-3, );
        return my $get=$all{shift(@_) };
}

for my $i(1..$len2){
    for my $j(1..$len1){
        my $ij=$ss2[$i-1].$ss1[$j-1];# 合并一下，方便匹配
        my $h1=get_score($ij)+$score[$i-1][$j-1]; # 来源：对角线
        my $h2=$score[$i-1][$j]-2;# 来源：纵向
        my $h3=$score[$i][$j-1]-2;# 来源：横向
        $score[$i][$j]=max($h1,$h2,$h3,0);
        if($score[$i][$j]==$h1){# 最值来源于对角线	
			$back[$i][$j]+=1;	
		}
		 if($score[$i][$j]==$h2){# 最值来源于上面		
			$back[$i][$j]+=2;	
		}
         if($score[$i][$j]==$h3){# 最值来源于左边		
			$back[$i][$j]+=4;	
		}
        if($score[$i][$j]==0){# 三个方向的值都不大于0	
			$back[$i][$j]=0;	
		}
    }
}

my $max_score=0;# 寻找最大值并记录其位置信息
my $where_i;
my $where_j;
for my $i(1..$len2){
    for my $j(1..$len1){
    if($score[$i][$j]>=$max_score)
    {   $max_score=$score[$i][$j];
        $where_i=$i;
        $where_j=$j;
    }
}
}

my @max_all;# 存放比对结果的三维数组
get_back($where_i,$where_j);

sub get_back{
    my($bi,$bj)=@_;
while(1){
    if($back[$bi][$bj]==1){
        unshift (@{$max_all[0]->[0]},$ss1[$bj-1]);	
		unshift (@{$max_all[0]->[1]},$ss2[$bi-1]);
        $bi--;# 坐标值根据相应来源方向而更新，下同
        $bj--;
    }
    elsif($back[$bi][$bj]==2){
        unshift (@{$max_all[0]->[0]},"-");	
		unshift (@{$max_all[0]->[1]},$ss2[$bi-1]);
        $bi--;
    }
    elsif($back[$bi][$bj]==4){
        unshift (@{$max_all[0]->[0]},$ss1[$bj-1]);	
		unshift (@{$max_all[0]->[1]},"-");
        $bj--;
    }
    elsif($back[$bi][$bj]==0){ # Smith-Waterman算法回溯到得分为0处即结束
       last;
    }
}
print "\n";
}
print "Aligned sequence:\n\n"; # 打印结果

	for my $j(0..1){
		print @{$max_all[0]->[$j]};
		print "\n";
	}

---

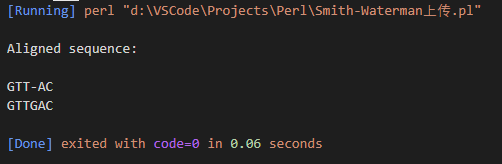
まとめ

虽说是分享代码但却发了不少牢骚，唉，上了生信的贼船也下不来了。凑合过吧。
mashiro_munetani 2022.11.13 WuHan City